curves.m |
Author: Paul Mennen Email: paul@mennen.org |

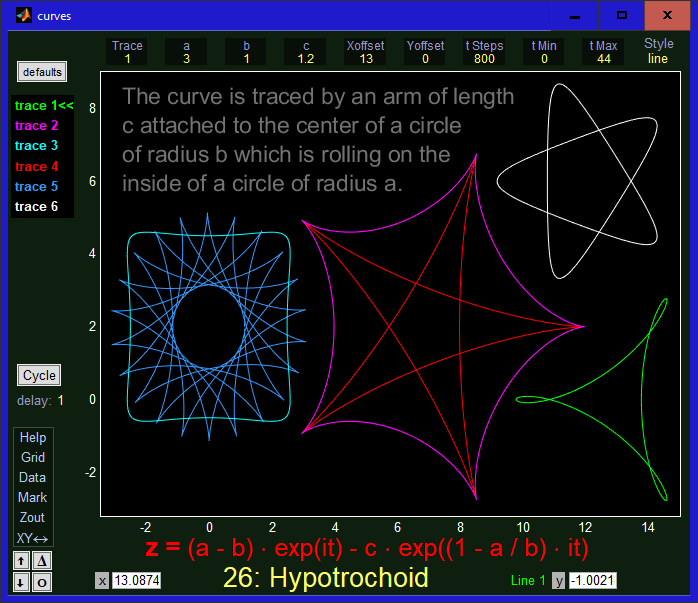 In this example, the equation defines the variable z, where z is always taken to be
a complex quantity. The real part of z will of course be plotted along the x axis and the imaginary part of z
will be plotted along the y axis.
In this example, the equation defines the variable z, where z is always taken to be
a complex quantity. The real part of z will of course be plotted along the x axis and the imaginary part of z
will be plotted along the y axis.