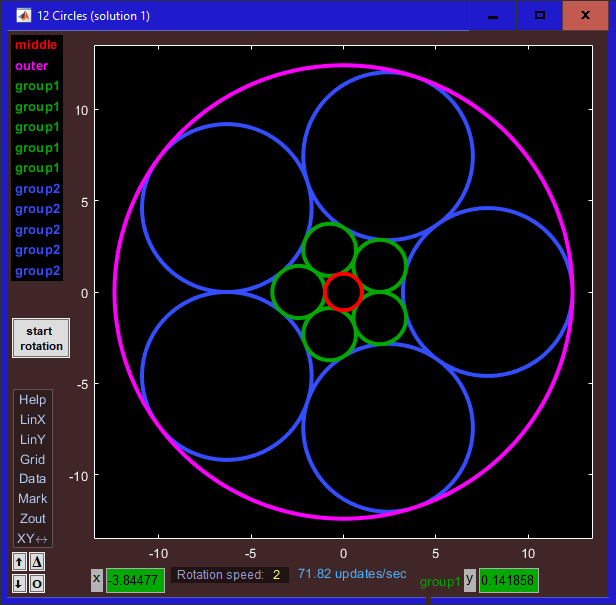
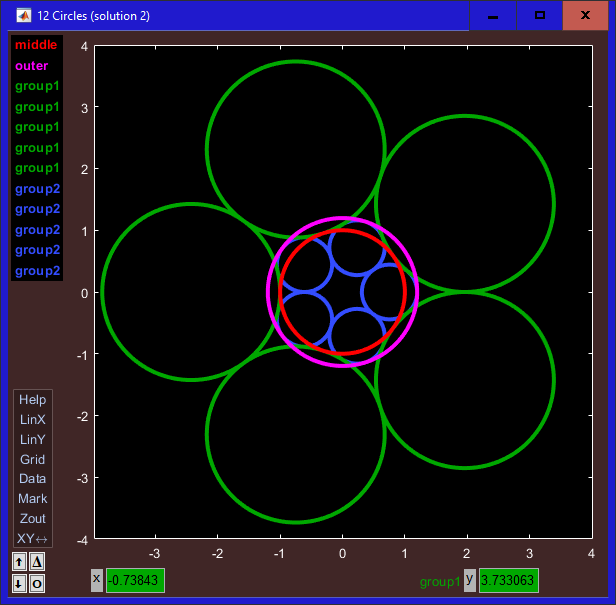
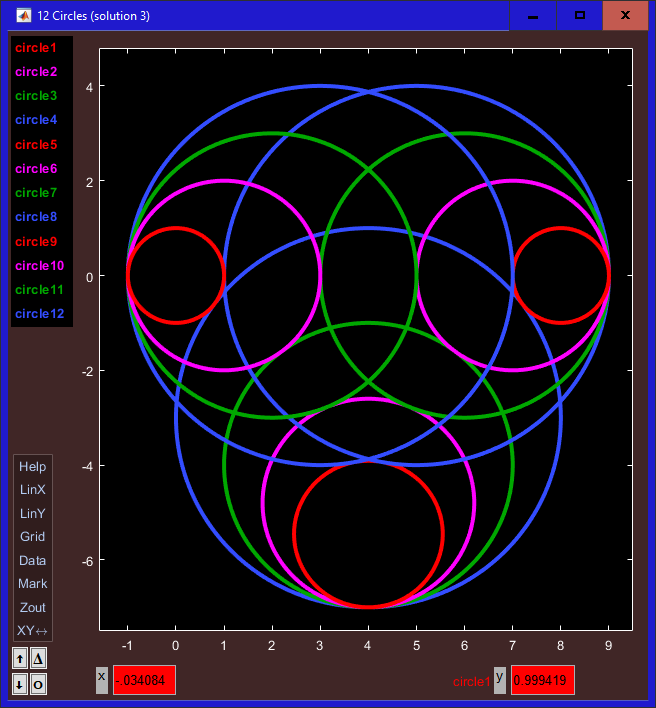
| • | Right click on the "Data" tag in the Menu box to make the menu bar visible |
| • | Click on "plt" in the menu bar and select "Hide/Show cursor controls" |
| • | Click on "plt" in the menu bar and select "Hide/Show TraceID box" |
| • | Click on "File" in the menu bar and select "Save As" and then select "Scalable Vector Graphics file" in the "Save as type" popup menu at the bottom |
 (This is a thumbnail image. Click on it to see the full resolution .svg image)
(This is a thumbnail image. Click on it to see the full resolution .svg image)